1. Polynomial Interpolation Examples

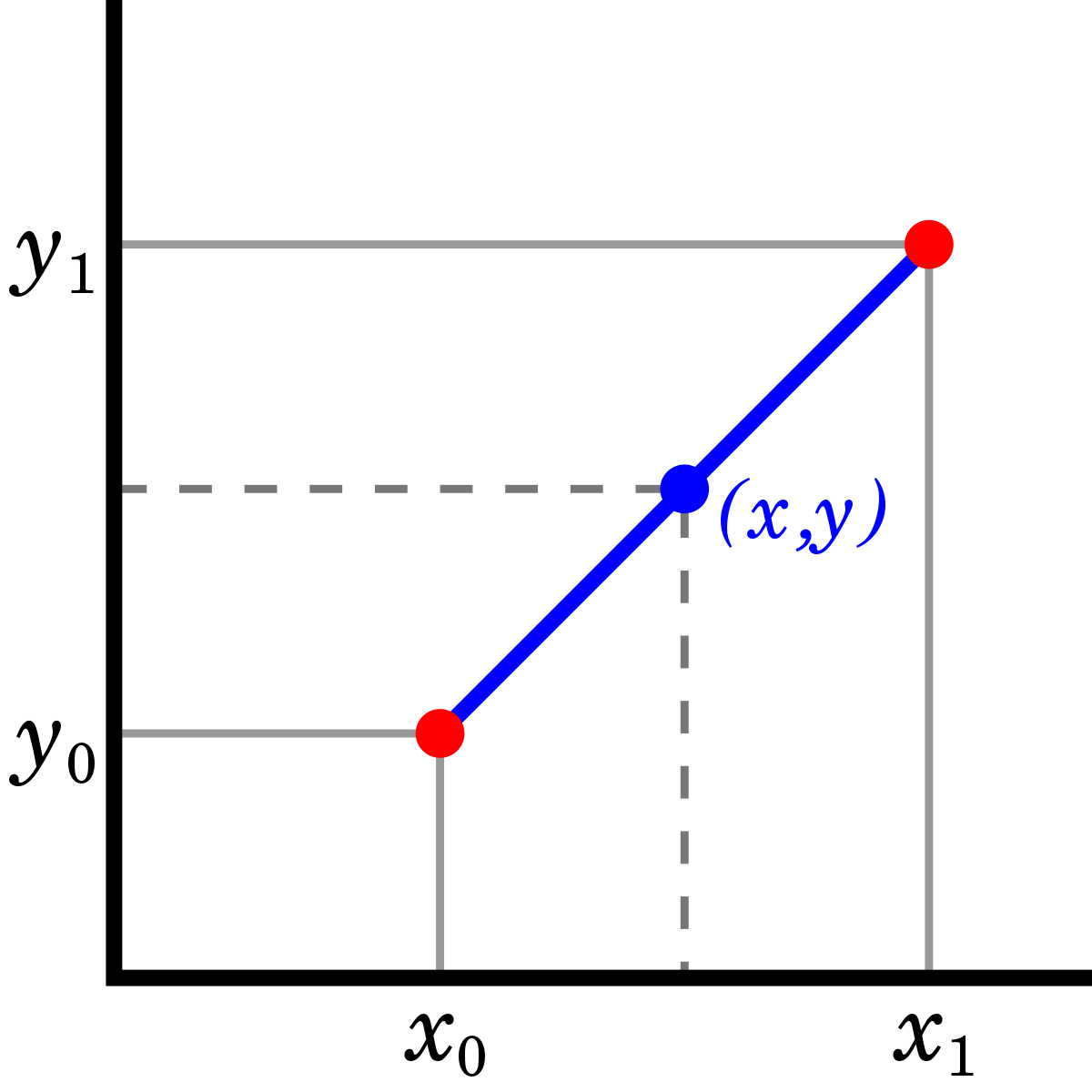
In on the forum, someone wanted to know how to find in-between values of a function, given some known data points. The approach, of course, is to interpolate values given the known points on either side of the value you need.Interpolation requires some simple algebra. The diagram below shows two points (blue diamonds connected by a blue line) with coordinates (X1, Y1) and (X2, Y2). We need to find the value of Y corresponding to a given X, represented by the red square at (X, Y).The smaller triangle with hypotenuse (X1, Y1)-(X, Y) is “similar” to the larger triangle with hypotenuse (X1, Y1)-(X2, Y2), so the sides of the triangles are proportionally sized, leading to the first equation below the sketch. We rearrange this to solve for Y, in the second equation.We’ll set up our interpolation in the example below.

Our data is in A5:B18, and the known values are plotted as blue diamonds connected by blue lines in the chart.The analysis has two parts: first we need to determine which pair of points to interpolate between, second we need to do the interpolation. We will judge the validity of our interpolation by plotting the calculated point on the same chart.Solving for YI’ve put the calculations above the data table. The yellow shaded cell, A2, holds the known X value, and a formula in cell B2 holds the calculated Y value. Cell A3 indicates which pair of points to interpolate between. The formulas are:A3: =MATCH(A2,A6:A18)B2: =INDEX(B6:B18,A3) + (A2-INDEX(A6:A18,A3)). (INDEX(B6:B18,A3+1)-INDEX(B6:B18,A3)) / (INDEX(A6:A18,A3+1)-INDEX(A6:A18,A3))We want the Gauge value (Y) when the Flow value (X) equals 3, so this is entered into the yellow shaded cell A2. The formula in A3 tells us that our computed point is between the 7th and 8th data point, and the formula in B2 calculate Y=0.444, and the calculated point (A2, B2) is the red square that lies along the plotted data points. Looks good.Te determine the Gauge value for a Flow value of 12, we enter this into A2.

The red square moves along the blue line past the 11th point, where Gauge=0.548.Solving for XWith a minor rearrangement, we can instead solve for Flow, given a value for Gauge. The known Gauge value is entered into B2, shaded yellow. B3 indicates the pair of points to interpolate between, and A2 provides the value for Flow. The formulas are:B3: =MATCH(B2,B6:B18)A2: =INDEX(A6:A18,B3) + (B2-INDEX(B6:B18,B3)). (INDEX(A6:A18,B3+1)-INDEX(A6:A18,B3)) / (INDEX(B6:B18,B3+1)-INDEX(B6:B18,B3))For a Gauge (Y) of 0.53, we compute a Flow (X) of 9.790. The red square shows where the calculate point lies along our plotted data.Changing the Gauge value to 0.35 moves the red square way to the left, to a Flow value of 0.400. Well, yes, of course.

I guess my point was badly made and my real question badly asked.If the data turns out to be just badly sampled, say it was some high frequency sine wave and you happen to sample at the right points, your data could look like a flat line would be the best fit line. So perhaps a linear estimation of the point you want to estimate, given the poorly sampled data, would not be the best way of going at it. 99 times out of a 100, though, it probably will.The nice thing about trendlines is you can see how good your fit is to the data fairly quickly. We could use all sorts of ways to more accurately figure out the function that the data actually seems to conform to, but Trendlines seems to do this quickly if not precisely.Is there some Trendline object that we can get at to get that nice little formula that you can have put onto your chart when you use Trendlines?

I since have played with it and found that there is ActiveChart.SeriesCollection(1).Trendlines(1).DataLabel.Text is what I was looking for. As it is text, you’d have to parse it and so it might be easier to do the other methods you mentioned, but it might be doable.Anyways, that’s what I was badly referring to.ikkeman says. After posting the trend I wondered:I’ve spend many hours trying to find a nice, concise way to do quadratic or cubic interpolation.Of course it’s possible to use linest to find the formula variables but is there another way?btw, another nice feature of the trend function is that is allowas you to do multiple variable linear interpolation.When you have a graph with multiple lines for different conditions (say your flow/guage ratio is dependent on temperature.

You can find the four points bracketing your search condition using the match function, and then input a 2×2 matrix as you input X, and a 1×2 as your target X and watch the magic happen!.Calvin Graham says. DaleW – Happy to share, took a while to figure out! It’s a little known fact that you can convert nearly any array formula to a non-array formula with MMULT, egArray =SUM(IF(A1:A52,B1:B5)) Non-Array =SUM(IF(MMULT(N(A1:A52),1),B1:B5))The straight/smooth chart line options have the property that they maintain the same shape if the configuration of points is rotated.

This can be seen in the formulas since X on Y followed by Y on X returns the original result with the linear/spline options, but not for trend or Lagrange polynomials (not Legendre, always get those guys mixed up!) VBA code for chart data isSplines have the intuitive appeal that they model the shape taken up by a smooth thin flexible strip passing through the set of points. In the linear case, the strip is pulled taught whereas in the cubic case there is no tension at the endpoints.DaleW says. Ihem – Interesting, I’d never seen MMULT used to replace an array formula. In real life, we’d both use =SUMIF for your example to have error checking, as otherwise a string entry in column A gives what we’d typically consider a bug.

MMULT does duplicate even such features.Natural cubic splines or Catmull-Rom cubic splines for exactly 4 points would follow your zero tension at the endpoints analogy. Other interpolating cubic splines have tension. Cardinal splines use piecewise cubic polynomials with a tension parameter ranging from 0 (for Catmull-Rom) to 1 (where they collapse to piecewise linear interpolation).

Thus Cardinal splines can replicate straight/smooth lines, or anywhere in between.lhem says. Hi,I’m no mathematician but i have tried my best to follow your logic.I was wondering if there was a way to Interpolate a point on a line between 2 known points. Not knowing the X or Y value? Example of data:X Y1 6.3 2.122 7.6 2.193 8.6 2.194 9.6 2.16On a Scatter with Smooth Lines & Markers graph the peak of the line will be between point 2 & 3. Is there a way to Interpolate that point?

(manually graphing it would give me an interpolation point of X=8.0 & Y=2.20) (X rounded to 0.5)I appreciate your assistance in this matter!Daniel.says. Daniel –You want to find where the smoothed drawn line has its maximum?

I usually advise people not to use smoothed lines. They give a false indication of where data may go. They are not based on any physical model of the data, but only on artistically connecting all points in a pretty way, using curve-drawing parameters that “looked nice” to the same kind of designer that gave us Excel’s early color palette.

Smoothed lines ignore any measurement error in the data which is actually present, they ignore all points in the data set other than the two being connected and the point on either side, and if markers are not displayed the viewer has no idea where the actual data lies.That said, for symmetric points, the usual approach is to fit a quadratic curve (2d order polynomial) to the points, and calculate a maximum using the fitted coefficients. A quadratic fit is probably reasonable, since physical processes often can be modeled by linear and quadratic relationships.Your points are not symmetric, so the fitted parabola does not pass through all the points; instead it lies in such a way as to minimize the total deviation of the parabola from the data points.

You could fit a third order polynomial to your data and calculate your maximum, but this starts to get into the realm of overfitting.DaleW says. Daniel,Realistically, close to X=8 is your best guess for the maximum.If you had really accurate measurements, an approach known as cubic splines would be great for fitting a smooth curve exactly to your data.

In fact, the smooth lines that Excel charts draw are one type of cubic spline.With four points, Excel can fit a cubic (3rd order) polynomial smoothly and exactly through the points. If you play with that equation, you’ll see it predicts the maximum at just over 8.08, and some people would consider that the best answer. (It’s really close to the natural cubic spline solution, also.)Jon’s right that anything past a linear fit without a physical model or lots of supporting data is risky or wishful thinking.

But if we are convinced that the data is highly accurate and don’t have a model, cubic splines are commonly used to create the smooth interpolating curve. In Excel, if we have two nearest neighbor points on each side of the region of interest, a cubic polynomial tends to be a very close approximation to the cubic spline fit there.Tshepo Phutha says. Tshepo –Did you change the formulas to include your whole data range (mine stopped at row 18, yours continues to row 22)?Cell A2 is where you enter an X value for which you want to calculate a Y value. It should not contain an error. What X value were you entering?Was the error in cell A3?

Was it because the requested X value was outside of the range of your X data?A more effective approach for your data might be a power law fit: such a fit with your data has an R² value of 0.9991.Tshepo Phutha says. Tshepo –So:B2 has the known YB3 =MATCH(B2,B6:B22)A2 =INDEX(A6:A22,B3) + (B2-INDEX(B6:B22,B3)).

(INDEX(A6:A22,B3+1)-INDEX(A6:A22,B3)) / (INDEX(B6:B22,B3+1)-INDEX(B6:B22,B3))But my formula assumed the range being matched was monotonically increasing, which I never stated. If I include the default value of the optional third parameter, the formula is=MATCH(B2,B6:B22,1)which tells Excel the data is increasing and to return the index the closest value greater than the sought value. Your formula needs to be=MATCH(B2,B6:B22,-1)which tells Excel the data is decreasing and to return the index the closest value less than the sought value.I still suggest using a power law fit.Tshepo Phutha says.

Hi Jon,I’m also finding a very strange error using the spline interpolation formula. I am interpolating the following set of data:xy1.1.2.2.2.596625772844656565983.86936435705873718429-14.391663062-14.469707695-14.547752328-24.601783228-24.667820995-24.733858761-34.787889661-44.841920561-44.895951461-44.949982361-5.376226126-65.394236426-65.40023986-6When I interpolate, I find that the following x values generate a #NUM! Error:4.901954894All the other values I am trying (less than and/or greater than these, and one in between the first two) seem to interpolate fine.The x values at which I am trying to interpolate are part of series of data. I am doing a calculation for some y values, and then interpolating the remaining x values. When I make small changes to the x value range, or use a different number of calculated points, there is often no problem at all.

Like the example above, the y values follow a generally decreasing trend, but this is not always the case and y may go up and down. The x values are always monotonically increasing.Let me know if you want any additional info. Thanks for any help you can provide in diagnosing this. It is a very vexing problem!-Charlie.CharlieL says. Ooops, a correction the “Legendre” formula seems to work just fine.

I discovered an error that I had made when entering it. The Spline still does not work, however.I have created a spreadsheet with the data mentioned above, and a correction to the “problem” data points to help diagnose the problem. It contains the SPLINE and LEGENDRE interpolation formulas, and shows that the SPLINE fails when one of the problem x values is entered.You can download it at:Thanks for any help!!!!-Charlie.DaleW says. Hi CharlieL,Alas, this particular formula for this particular cubic spline indeed fails for part of your dataset.That segment of your Catmull-Rom spline happens not to be monotonic for predicting Y from X. This causes the IRR formula to fail rather interestingly in at least 5 subintervals of that segment’s range in X, for X values that are monovalent instead of trivalent!?While I was able to calculate and chart the real Catmull-Rom spline directly from its defnition as a t-function-weighted sum of the two nearest points in each direction in X, you possibly don’t want a spline that behaves this way to fit your dataset. Perhaps a natural cubic spline or a monotonically constrained cubic hermite spline would be a better choice? The Newton Excel Bach blog has done a wonderful job setting up VBA code to let Excel users explore a variety of different cubic splines.DaleW says.

Hi DaleW,Thanks for posting an explanation of the problem. I do need a worksheet-formula-only way to do the interpolation (e.g.

No VBA or macros), and I would like a smooth curve a la spline or similar. For now I have switched to the Legendre formula, and that seems to work OK for the type of data I am generating. I am still learning about how to implement matrix multiplication via the MMULT function, and I am not up to coming up with something new myself at this point, although I would like to learn how to do it. Also, it’s not clear to me whether the problem that I described in my post was due to a limitation of the Catmull-Rom spline itself, or the implementation via the formula. Can you please elaborate on this?I need the interpolated line to go through the points in the data set. You mentioned that this is the “wrong” spline – how about a B-Spline?

For instance, the Uniform Cubic B-Spline described here:has an explicit matrix form that seems to lend itself well to this approach (from what I can tell). Can you (or someone else reading this post) help me implement it using IIR and MMULT?Thanks!-Charlie.DaleW says. Charlie,B-Splines don’t go through their control points, which is inconvenient when you want to interpolate actual data.Catmull-Rom splines do interpolate their control points, but they aren’t constrained by the concept that there should be one and only one Y value for each X value. I believe some IRR problems have more than one rate of return that solves the constraints, but a “well-defined” mathematical function can only return one value for a given value of X. Thus IRR fails to capture parts of some Catmull-Rom spline segments, which a weighted sum of the control points in terms of a t parameter going from 0 to 1 in each segment does reveal.Assuming you’d like a “well-defined” and smooth continuous interpolating function for Y on X, I would recommend the classic solution of natural cubic splines. Usually this is implemented in programming languages, and I’ve got more than one VBA solution squirreled away. I don’t imagine that solving the sparse symmetric matrix equations for under 50 points would be that hard to program using the cells of a spreadsheet, if one were so inclined.The Legendre formula is the cubic polynomial solution, or the simplest natural cubic spline case.

The Legendre formula will not give you continuous derivatives if you use it for more than 4 total points. In one mathematical sense, natural cubic splines offer the smoothest possible interpolation. Natural cubic splines aren’t likely to be used for graphics because it isn’t a local solution like Legendre or Catmull-Rom, and every point instead of just 4 local points can have some impact every segment of the spline, making it more computationally intensive.CharlieL says.

Charlie,Good enough!Incidentally, your dataset can be used to show that Excel must modify the Catmull-Rom spline algorithm to draw its smoothed lines, because Excel smoothed lines usually overlap that spline yet avoid the pathology that you found. As Answers.Microsoft notes, “An adjustment to the basic method is applied if consecutive points are a factor of three or more apart so as to reduce the amount by which the curve overshoots points.” I interpret this as a sort of false position method, where any outer control point that further that 3x the distance between the inner control points is pulled closer. Thus on your troublesome (X,Y) interval between (4.895951461, -4) and (4.949982361, -513.475427), the next point is treated as if it were closer at (5.2305,-600.2523) for the purposes of the Catmull-Rom algorithm on that segment only, which removes the strange behavior and restores single-valued functionality and lets the IRR formula work, as well as duplicates the Excel smoothed line exactly on my plot. This might be more trouble than it is worth for you to duplicate Excel’s native interpolating spline — but it would be a lot easier than solving the tridiagonal matrix equation for natural cubic splines. You’d just need to create a table of the 4 XY control points for each of N-3 inner segments where you say your full table is N=600, and the Catmull-Rom OFFSET logic would have to point to that table. This would provide C1 continuity (of 1st derivatives), but not the C2 continuity (of 2nd derivatives also) that is provided by natural cubic splines.

Your Legendre solution only has C0 continuity (of the function itself) at the data points (but C2 continuity elsewhere like all cubic splines within each segment, not necessarily between segments).BTW, are you sure you want spline interpolation instead of LOESS smoothing?.says. Jon – yes, I saw that. I believe that the Bezier algorithms may be very similar, but MS Excel actually uses modified Catmull-Rom splines, per the July 4, 2011 post by Answers.Microsoft in response to Tushar Mehta. The VBA code is there, but I think that I did duplicate quickly the Excel charting smooth curve for this troublesome case by using a false position for a far outer control point as I tried to describe using both Catmull-Rom formulas (the quick IRR one discussed on your blog, and the formal definition in terms of weighted sums of the 4 basis points using t-parameter polynomials).DaleW says. I’ve been trying to get this to work with a very small set of yearly data so:X = year in the format 2001Y = a priceI have this data for 12 yearsi want to estimate a monthly value in any of those twelve years.However, i’m struggling to do this with your spreadsheet.For example i tried 2001.083 which could predicate a monthhowever i get a ref error in A2 and i dont think this is the best way of doing it.Ultimately i want to try and estimate each monthly figure based on a set of yearly final figure. So the value of months 1 through 12 should equal the current yearly figure.Hope this makes sens.e.says. Maak –I presume you want a new Y value for each X value in your second list.I put the pairs of X and Y into X-Y order, not Y-X order (columns A:B, see screenshot below).I put the new X values into another column E.I used column D for an index, which points to the value in the column of input X values closest to but greater than the new X value.

The formula in D2 is as follows, and copied down as far as there are values in column E:=MATCH(E2,$A$2:$A$181,-1)The third argument, -1, is needed because the input X values are in decreasing order.I used column F for the interpolated Y values. The formula in F2 is as follows, copied down as far as needed:=(E2-INDEX($A$2:$A$181,D2))/(INDEX($A$2:$A$181,D2+1)-INDEX($A$2:$A$181,D2)).(INDEX($B$2:$B$181,D2+1)-INDEX($B$2:$B$181,D2))+INDEX($B$2:$B$181,D2)It’s basically the same formula as in cell B2 of the example.wga says. Hi,I see that the graph never fall back (it ascends). But what if when the curve falls back (quadratic – so that each y value will have two x values). How can we interpolate for x for a given y value? Given: y=0.61357555The correct answer is x=8 with this formula: =A20+((L3-B20)/(B21-B20)).(A21-A20). But I don’t need to manually search for the lower and upper bounds of the given value in y and corresponding x.

I need the first (smaller x value).Thanks,Here is the data.y x37.188.275.830.560.36296.84595.25920.18206.45507.82784.48966.22082.94222.232.wga says. Anant –Good point. Interpolation gives us the coordinates of a point on a straight line between two known points. But we get a different straight line depending on our coordinate system. The straight line we get using linear X and Y (blue in the charts below) is not the same as the straight line we get when our X axis is logarithmic (orange). These are the last two points of your input data, sorted in increasing order or particle size.We need to use a modification to our formula if we want to capture the logarithmic straight line.

Hi all,My name is Gabriel, I am doing a phd in biomechanic applied to tennis. I have created an excel spreedsheet to analyze tennis strokes in 3d (using an algorithm called direct linear transformation). Now I hace the x, y, z coordenates of one relevant point of the tennis racquet.

Knowing the time between frames I want to compute the speed. I want to compute the speed by differentiation of the position. The easiest way is to use the position of two adjacent point but I want to do something more advanced and conpute speed differentiating cubic splines.

Polynomial Interpolation Examples

In biomechanic quintil splines are usually used but I have never seen they implemented in excel. I think cubic splines are also a good solution. I want to do this by using not array formulas but I do not know if it is possible. I think this forum is perfect for asking it as I have seen (but not understand) fantastic formulaes using not array functions. If you think there is an easier way to do this (althought is not the perfect solution) please tell me. One colleague also told me that when the time between frames was not exact (in my case the camera records at 120 hz so the time has periodic decimals) all this proccesed were more complicated (but I think he refered to the application of the IRR filters). As you can deduce by my message I need a dummy solution.Thanks a lot,Gabriel.says.